Latest Projects
These are all the projects I've worked on or currently working on. That includes class project, personal project, or group project.
Independent Set
Have you ever wonder how social media works? How many people have to share an announcement for everyone on the network to see it? Well, you have found the right person to answer your question.
The maximal independent set problem explored in this program is a NP-hard optimization problem. A greedy approach and a backtracking approach were used for the maximal independent set problem.
Have you ever wonder how social media works? How many people have to share an announcement for everyone on the network to see it? Well, you have found the right person to answer your question.
The maximal independent set problem explored in this program is a NP-hard optimization problem. A greedy approach and a backtracking approach were used for the maximal independent set problem.
The maximal independent set problem explored in this program is a NP-hard optimization problem, so optimal solutions are not likely to be efficient.
Functions
buildGraph:
Builds a random undirected graph where each possible edge is in the graph with probability 1/2 based on the number of nodes we pass in as a parameter.
printGraph:
Given a graph, print out the content in the C++ vector.
independentSet:
In this function, we implemented a greedy algorithm for maximal independent set based by including nodes of smallest degree. However, the greedy algorithm does not always find the best solution.
Run Time: $O(n)$
independentSetBT:
Instance (Input): Undirected Graph
Solution Format: Subset of the vertices
Constraint: No two vertices are connected with an edge, For each edge e={u,v}, if u is in S, v is not in S.
Objective: Maximize the size of the subset.
Solution Space: all subsets S of V, |V|= n, number of nodes .
Exhaustive search: $O(2^n)$
Backtracking: Do exhaustive search locally, but use constraints to simplify problem as we go.
What is a local decision? For an arbitrary vertex u, is implemented part of the optimal solution or not.
What are the possible answers to this decision? Yes or No
This is implemented with a backtracking algorithm, with constraints to prune cases that have a dead end, thus giving us a more efficient algorithm compared to an exhaustive search.
Although much slower (running in sub-exponential time) than the greedy algorithm, the backtracking algorithm gives the actual size of the maximal independent set in a random set.
Run time: $O(2^{0.6n})$
Testing
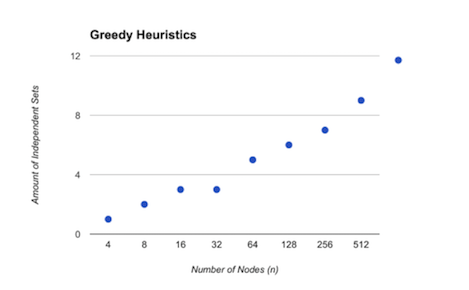
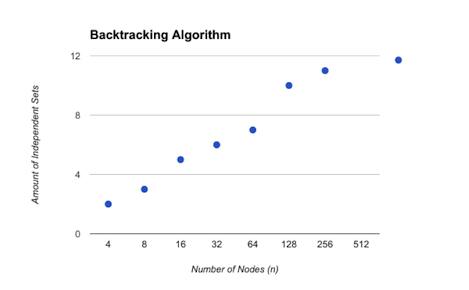
These two functions are being tested on the randomized graph generated by the buildGraph method. With the data recorded below, it shows that the backtracking algorithm consistently finds a larger independent set, at the rate that’s double of the size of independent set greedy algorithm finds on the same “randomized graph”, which is an indication that it’s giving us the optimal solution as discussed in class.
| Greedy Heuristic | Backtracking Algorithm | ||
|---|---|---|---|
| Nodes (n) | Number of Independent Sets (|S|) | Nodes (n) | Number of Independent Sets (|S|) |
| 4 | 1 | 4 | 2 |
| 8 | 2 | 8 | 3 |
| 16 | 3 | 16 | 5 |
| 32 | 3 | 32 | 6 |
| 64 | 5 | 64 | 7 |
| 128 | 6 | 128 | 10 |
| 256 | 7 | 256 | 11 |
| 512 | 9 | ||
Extension
This is a real-life application using the independent set algorithm, which is a use of the minimum spanning set.
Problem:
Given a data set of all users on Twitter/Facebook or any social media, assuming announcements made by a user will be seen by all their followers, find how many users are required to make the announcement for all the people on the same network to see the announcement. Therefore, given a graph, find a subset of vertices, S, such that every vertex not in S is adjacent to at least one vertex not in S is adjacent to at least one vertex in S.
How we solved it:
We have implemented a simple greedy algorithm, and to find the dominant set of vertices and return it. To do that, we marked all the vertices as "uncovered" in each User's constructor. We then initialize an empty vector. While the number of covered edges is not the same as the number of vertices in allUser, then we iterate through allUser to find the user vertex with the most followers, also if a vertex cover field is true, then we simply increment the amount of covered vertex and continue with the loop without trying to find the vertex.
Once we have found the vertex user with the most followers, we add it to the dominant set we have initialized and simply set its covered field to true, and we loop through its followers, find the followers in allUser and set their covered field to true as well. Then at the end, we return the sets with all the vertices that were used to cover the entire graph.
How we tested our program:
I came up with some general test cases, the first being smallgraph.tsv, it contains 4 nodes, 1-(3), 2-(3,4), 3-(1,2), 4-(2). The 1, 2, 3, 4 are vertices of the graph, and - denotes edge relationship. It is a directed graph.
Therefore, we are trying to figure out how many nodes I have to explore before all the users are reached by the announcement, assuming that all the nodes that are directly connected by the announcer will see the announcement. We find that Node 2 has the 2 edges, which is the most, so does Node 3 but it doesn't matter in this case. We explore and set 2, 3, 4 all to true. Then we see Node 1 is the only vertex that has yet to be explored.
Thus, the output file tells us that User 2 and 1 has to announce the news so that all the nodes will see it. Of course, other answers exist, but this algorithm's simply tasked to find one solution, not all the possible solutions, nor the optimal solution.
Same goes for smallgraph2.tsv, in which there are Node 1, 2, 3, 4, 5, 6, 7, 8. In which all nodes are connected to 1, but 6, which is only connected to 2. Therefore, we know the answer has to either be 1,6. Node 1 must be explored because it has the most edges, and afterward, 2 through 8 with the exception of Node 6 are all explored. Then we go and explore Node 6. In our output file, it gives us the correct output.
How to run this program:
To run the program please use the following command.
./extension file1 file2
For example:
files provided by me
> ./extension smallgraph.tsv test.tsv
> ./extension smallgraph1.tsv test1.tsv
Where column1 is the user number, and the column2 is the user that is a follower of the user in column 1. C1 and C2 are divided by a space. The data provided do not need processing.
Project Type:
Tip Easy
Don’t have a good tip calculator app on your phone? Tired of tipping the post-tax amount? Or you are just like me who tips the pre-tax bill just out of habit. Well, you have found the right app. This is an iOS app that takes in the user’s location to see the tax rate of the location and calculate the right amount to tip your waiters based on the pre-tax bill.
Don’t have a good tip calculator app on your phone? Tired of tipping the post-tax amount? Or you are just like me who tips the pre-tax bill just out of habit. Well, you have found the right app. This is an iOS app that takes in the user’s location to see the tax rate of the location and calculate the right amount to tip your waiters based on the pre-tax bill.
What did I learned? I learned the basics in Swift, such as View Controller, i.e. label, text, segmented control, button, number pads.
I used the CoreLocation framework in Swift as well as the interfaces of CLGeocode and CLLocationManager.
CLLocationManager was used to extract the user’s location, i.e. longitude and latitude. CLGeocode was then used to take in the user’s location and extract the zip code of the user’s current whereabouts. So I can use it to look up the sales tax rate.
I found the data of sales tax rates by locations here. After doing some minor clean up of the data to turn it into a form that would be useful to the applicaiton, I wrote a short python script to process data. I then read in the data and created a database using SQLite.
Finally I incorporated the SQLite database into Swift by using a wrapper, so I could make sales tax rate lookups very efficiently.
Project Type:
2048 Mod
2048 is a puzzle game played on a simple grid of size 4x4, with numbered tiles that are a power of 2. The numbered-tiles slide in one of 4 directions based on user input. Every turn, a new tile will randomly appear in an empty spot on the board with a value of either 2 or 4. Tiles will slide as far as possible in the desired direction until they are stopped by another tile or the edge of the grid. If two tiles of the same number collide while moving, they will merge into a tile with the total value of the two tiles combined.
This is a modification of the game 2048, a popular puzzle game in the app store where a player's goal is to create a tile of 2048. The original game can be found here.
2048 is a puzzle game played on a simple grid of size 4x4, with numbered tiles that are a power of 2. The numbered-tiles slide in one of 4 directions based on user input. Every turn, a new tile will randomly appear in an empty spot on the board with a value of either 2 or 4. Tiles will slide as far as possible in the desired direction until they are stopped by another tile or the edge of the grid. If two tiles of the same number collide while moving, they will merge into a tile with the total value of the two tiles combined.
This is a modification of the game 2048, a popular puzzle game in the app store where a player's goal is to create a tile of 2048. The original game can be found here.
Some modifications to the game:
Upon exit, you can save the board, and you can load a board you've saved prior.
You can create a game board of size 4 or bigger.
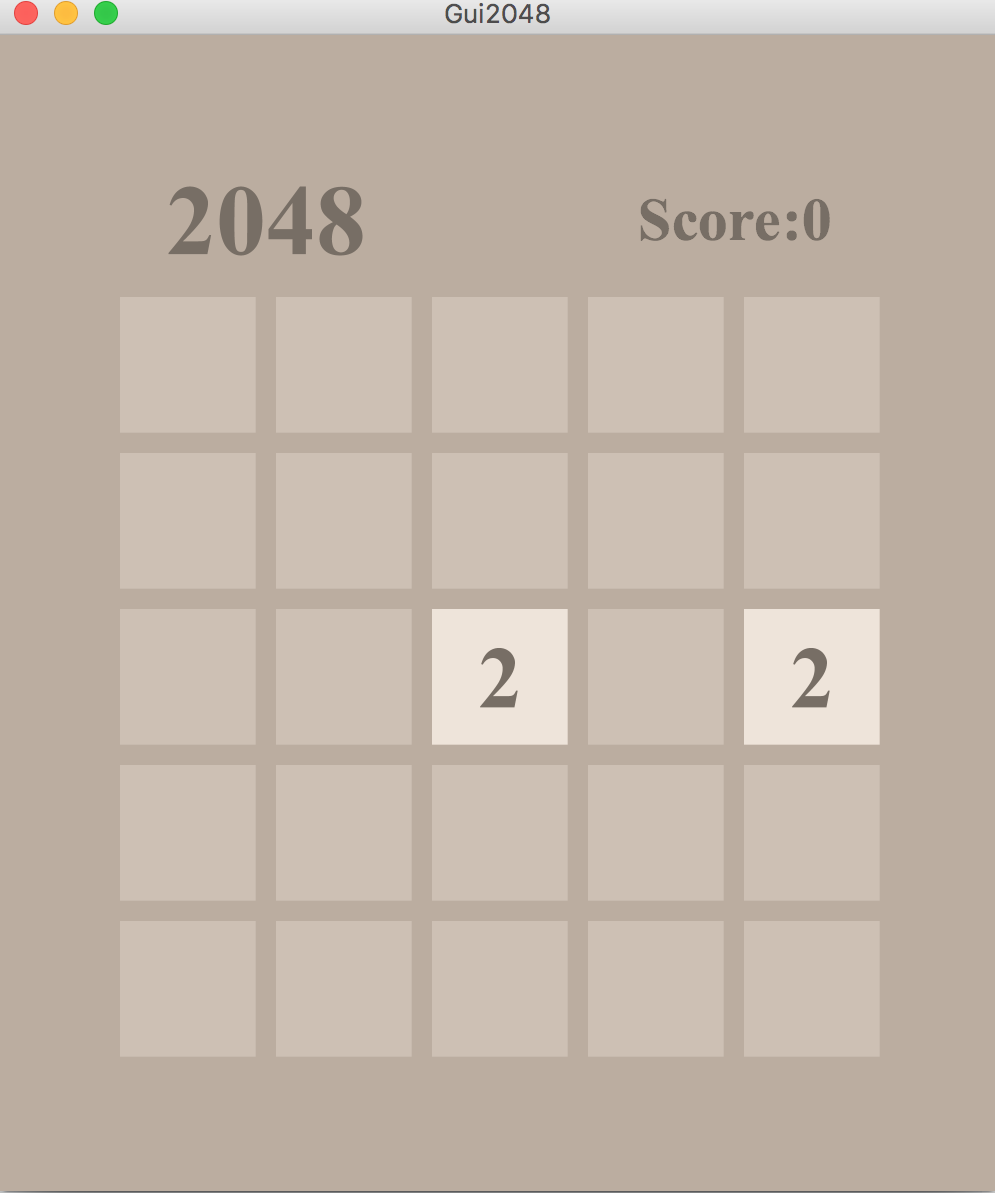

You can rotate the tiles on board clockwise by 90 degrees with the rotate key, r.


To compile:
>javac GameManager.java Gui2048.java Board.java Direction.java
To run the program:
Ex:
>java Gui2048 -o my2048.board -i input2048.board
>java Gui2048 -s 5
>java Gui2048
Input Tags
-i filename - used to specify an input board
-o filename - used to specify where to save the board upon exit
-s integer - used to specify the grid size
Project Type:
CSVR
This is a virtual reality experience and an education tool where you can learn a lot of concepts and data structure of computer science. I implemented the back end and the design of interactive data structure, such as stack and hash table in three different collision strategies in Unity using C#.
This repository is private for this ongoing group project.
This is a virtual reality experience and an education tool where you can learn a lot of concepts and data structure of computer science. I implemented the back end and the design of interactive data structure, such as stack and hash table in three different collision strategies in Unity using C#.
First I would like to highlight our accomplishments this quarter. We have successfully implemented many data structures visualizers and made them interactive.
My personal contribution to the team was that I was in charge of the back end coding as well as the basic visualization. I have implemented a stack using List in C# with functions such as insert, remove, and lookup. On top of that, preserve characteristics such as First-In-First-Out. It can be seen that when we insert, it adds a block to the scene when we remove it pushes a block to the side, and when we look up, it highlights and changes the color of the block that’s on top of the stack. I have also implemented a hash table using linear probing collision strategy with its basic functions, hash function, insert, lookup, and remove.
Some challenges I have faced was definitely time management on the project. Although it does not seem too time-consuming to implement. I am fairly new to unity, C#, and VR development. Therefore, the learning curve was undeniable. On the side, I have played around with Unity elements such as implementing the tutorial Roll A Ball Game. Even on top of that, I also tried to pick up more knowledge of unity by making a 3D PacMan Game using the base model created with the Roll A Ball Game. It is also hard to allocate time to do this project on the side on top of school work. Thankfully, I have really helpful and knowledgeable team members who are always willing to help me out.
There are some setbacks this quarter. Since I am fairly new to this development environment. Therefore debugging my code was a relatively difficult task. It sometimes takes days just to find a bug in my code and wonder what’s not working. Through the challenges and setbacks, I have become a stronger programmer who debugs more efficiently.
This is a group project worked on under the supervision of Professor Jürgen P. Schulze. Here is the Final Report.
Stack
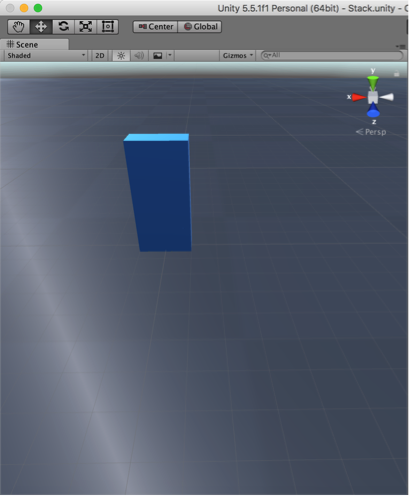
Pushing to the stack 4 times.
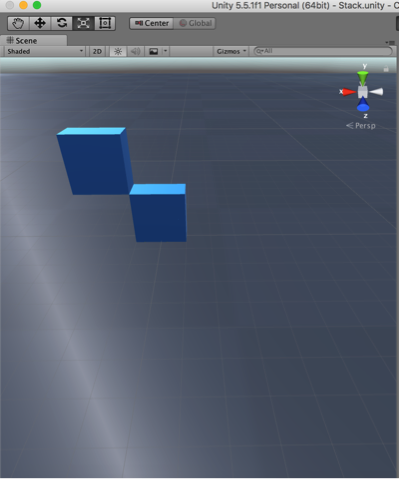
Pushing 4 times then pop twice from the stack.
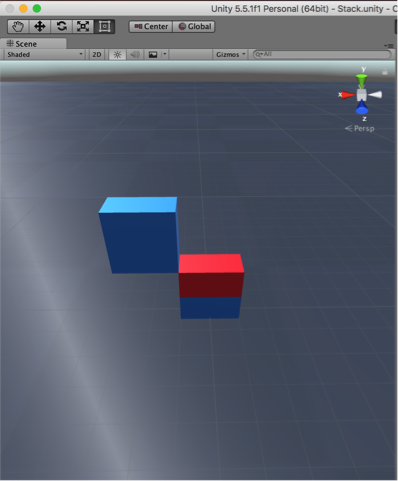
Calling the peak function highlights the top of the stack.
Hash Table
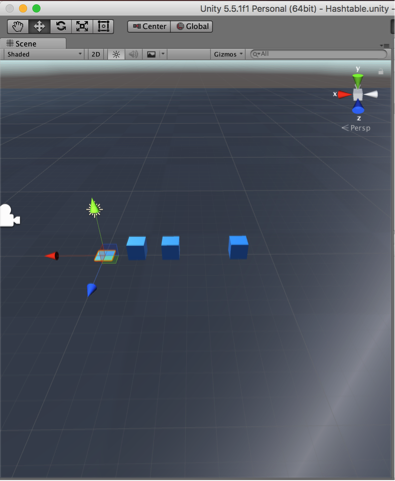
Size 11 hash table 1 after inserting 30, 15, and 13.
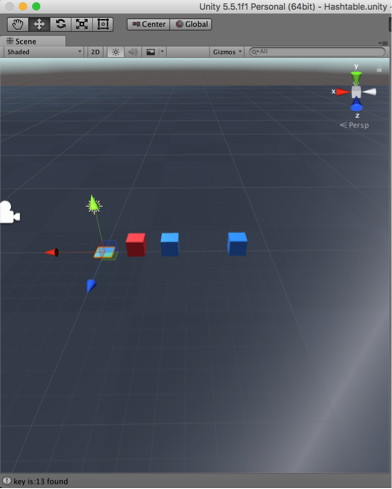
Finding 13 in the hash table 1.
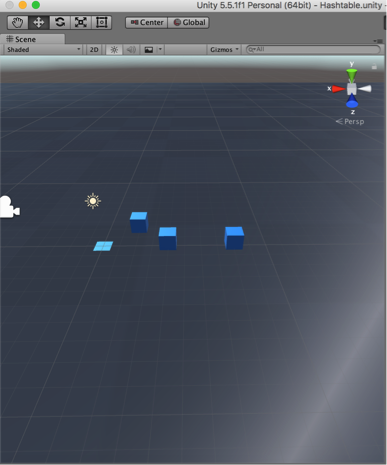
Removing 13 from the hash table 1.
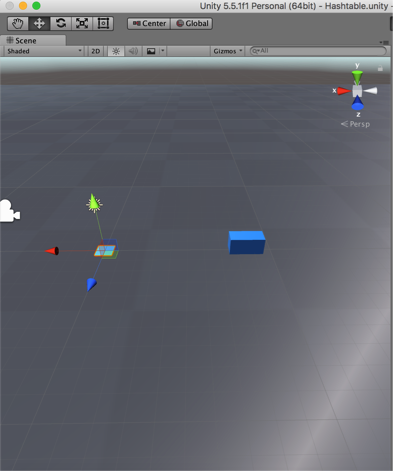
Size 11 hashtable 2 - Inserting 30, and 19 to check linear probing collision insert.
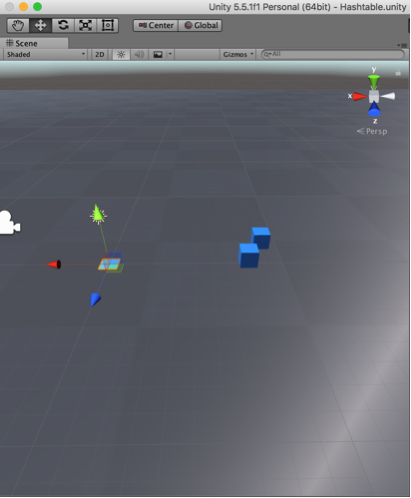
Removing 19 from hash table 2 to check linear probing delete.


